Definição Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a Vejamos alguns exemplos de função quadráticas:
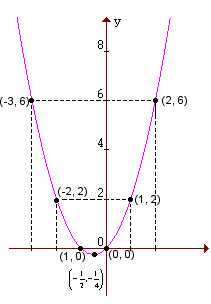
Gráfico O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a Exemplo: Vamos construir o gráfico da função y = x2 + x: Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
Observação: Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
Zero e Equação do 2º Grau Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara: Temos: Observação A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando
|
BOAS VINDAS !
SEJAM BEM VINDOS AO BLOG DA TURMA 1001
quarta-feira, 1 de setembro de 2010
Função Quadrática
Assinar:
Postar comentários (Atom)

COMUNICADO URGENTE!!!
ResponderExcluirO prazo para apresentação da atividade dos grupos é até o dia 20 de setembro de 2010. Lembrem-se que o trabalho vale 5,0 pontos e faz parte da nota do bimestre. Não percam tempo!!!!